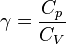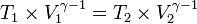Jendela Pengetahuan Fisika: November 2014

Teori Kinetik Gas

Di dalam teori kinetik gas terdapat suatu gas ideal. Gas ideal adalah suatu gas yang memiliki sifat-sifat sebagai berikut :

" Jumlah partikel gas banyak sekali tetapi tidak ada gaya tarik menarik (interaksi) antar partikel , Setiap partikel gas selalu bergerak dengan arah sembarang atau bergerak secara acak "

Ukuran partikel gas dapat diabaikan terhadap ukuran ruangan. Atau bisa dikatakan ukuran partikel gas ideal jauh lebih kecil daripada jarak atar partikel . Bila tumbukan yang terjadi sifatnya lenting sempurna , maka partikel gas terdistribusi merata pada seluruh ruang dengan jumlah yang banyak dan berlaku hukum Newton tentang gerak

Di dalam kenyataannya, kita tidak menemukan suatu gas yang memenuhi kriteria di atas, akan tetapi sifat itu dapat didekati oleh gas pada temperatur tinggi dan tekanan rendah atau gas pada kondisi jauh di atas titik kritis dalam diagram PT.

2. Hukum-hukum tentang gas
A.Hukum Boyle

Hasil kali tekanan(P) dan volume(V) gas pada suhu tertentu adalah tetap. Proses seperti ini disebut juga dengan isotermal (temperatur tetap).
*PV=konstan
*T2>T1
*Tidak berlaku pada uap jenuh

B.Hukum Guy Lussac

Hasil bagi volume(V) dengan temperatur (T) gas pada tekanan tertentu adalah tetap. Proses ini disebut juga isobarik (tekanan tetap).
*V/T=konstan
*P3>P2>P1

C.Hukum Charles

Hasil bagi tekanan (P) dengan temperatur (T) gas pada volume tertentu adalah tetap. Proses seperti ini disebut dengan isokhorik (volume tetap).

*P/T=konstan
*V3>V2>V1

D.Hukum Boyle-Guy Lussac

Hukum Boyle dan Guy Lussac merupakan penggabungan dari hukum Boyle dengan hukum Guy Lussac. Biasanya di dalam soal rumus yang sering digunakan adalah rumus dari hukum ini. Sekedar trik dari saya, anda bisa menamai hukum ini dengan hukum BoLu (Boyle-Lussac). Nah, dari hukum ini kita bisa mendapatkan: PV/T=konstan.

Persamaan Keadaan Gas Ideal

Contoh soal dan pembahasannya

1. Sebuah bejana berisi gas He yang mempunyai volume 2 L, tekanan 1 atm dan suhunya 27`C. Jika suhunya dinaikkan menjadi 127`C dan ternyata tekanannya naik 2 kalinya. Hitung volume sekarang !

2. Sebuah tangki bervolume 3000 cm3 berisi gas O2 pada suhu 20`C dan tekanan relatif pada alat 25 atm. Jika massa molar O2=32 kg/kmol, tekanan udara luar 1 atm, maka massa O2 di dalam tangki adalah …

Termodinamika

Hukum 0 Termodinamika: Jika dua sistem dalam keadaan setimbang dengan sistem ketiga, maka ketiga sistem saling setimbang satu dengan lainnya.
Hukum 1 Termodinamika: Berbicara tentang prinsip kekekalan energi yang berbunyi "Energi tidak dapat diciptakan dan tidak dapat dimusnahkan tetapi energi dapat diubah dari suatu bentuk energi ke bentuk energi yang lainnya".
Hukum II Termodinamika: Energi kalor tidak dapat seluruhnya diubah menjadi energi mekanik atau usaha, tetapi sebagian akan terbuang.
Hukum III Termodinamika: Suatu saat sistem akan berada pada suhu nol absolut, proses akan berhenti dan entropi sistem akan mendekati nilai minimum.

Hukum Pertama Termodinamika

Perubahan energi dalam:

\Delta U= U_2 - U_1

Keterangan:

$\Delta U$ :Perubahan energi dalam (Joule)
U₂:Energi dalam pada keadaan akhir (Joule)
U₁:Energi dalam pada keadaan awal (Joule)

Usaha yang dilakukan oleh gas pada tekanan tetap:

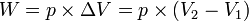
W = p \times \Delta V = p \times (V_2 - V_1)

Keterangan:

p: Besarnya tekanan (atm)
$\Delta V$ : Perubahan volume (liter)

Rumus umum usaha yang dilakukan gas:

W = \int_{v_1}^{v_2} p dV

Penghitungan energi dalam:

Gas monoatomik: $\Delta U = \frac {3}{2}n \times R \times \Delta T = \frac {3}{2}n \times R \times (T_2-T_1)$
Gas diatomik: $\Delta U = \frac {5}{2}n \times R \times \Delta T = \frac {5}{2}n \times R \times (T_2-T_1)$

Proses-proses termodinamika gas

1. Proses isobarik

Diagram proses isobarik. Daerah berwarna kuning sama dengan usaha yang dilakukan.

Proses isobarik adalah perubahan keadaan gas pada tekanan tetap.
Persamaan keadaan isobarik:

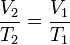
\frac {V_2}{T_2}= \frac {V_1}{T_1}

Usaha yang dilakukan pada keadaan isobarik:

W = p \times \Delta V

Proses isokhorik

Digram proses isokhorik. Grafiknya berupa garis lurus vertikal karena volumenya tidak berubah. Tidak ada usaha yang dilakukan pada proses isokhorik.

Proses isokhorik adalah perubahan keadaan gas pada volume tetap.
Persamaan keadaan isokhorik:

$\frac {p_2}{T_2}= \frac {p_1}{T_1}$

3. Proses isotermis/isotermik

Proses isotermik. Daerah berwarna biru menunjukkan besarnya usaha yang dilakukan gas.

Proses isotermik adalah perubahan keadaan gas pada suhu tetap.

Persamaan keadaan isotermik:

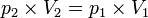
p_2 \times V_2= p_1 \times V_1

Usaha yang dilakukan pada keadaan isotermik:

Dari persamaan gas ideal

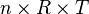p= \frac {n \times R \times T}{V}

Rumus umum usaha yang dilakukan gas:

W = \int_{v_1}^{v_2} p dV

maka:

W = \int_{v_1}^{v_2} \frac {n \times R \times T}{V} dV

karena

n \times R \times T

bernilai tetap, maka: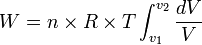

W = {n \times R \times T} \int_{v_1}^{v_2} \frac {dV}{V}

Ingat integral ini!

\int \frac {dx}{x} = \ln x

maka persamaan di atas menjadi

W = n \times R \times T \times[\ln V_2 - \ln V_1]

maka menjadi:

W = n \times R \times T \times \ln (\frac {V_2}{V_1})

4. Proses adiabatik

Proses adiabatik. Warna biru muda menunjukkan besarnya usaha yang dilakukan.

Proses adiabatik adalah perubahan keadaan gas dimana tidak ada kalor yang masuk maupun keluar dari sistem.

Persamaan keadaan adiabatik:

p_1 \times V_1^{\gamma} = p_2 \times V_2^{\gamma}

Tetapan Laplace:

\gamma = \frac {C_p}{C_V}

karena

p= \frac {n \times R \times T}{V}

, maka persamaan diatas dapat juga ditulis:

T_1 \times V_1^{\gamma-1} = T_2 \times V_2^{\gamma-1}

Usaha yang dilakukan pada proses adiabatik:

W = \frac {1}{\gamma-1} (p_1 \times V_1 - p_2 \times V_2)

Tumbukan

Tumbukan dapat berlangsung secara singkat dan dapat pula berlangsung lama. Pada semua proses tumbukan, benda-benda yang saling bertumbukan akan berinteraksi dengan kuat hanya selama tumbukan berlangsung kalaupun ada gaya eksternal yang bekerja, besarnya akan jauh lebih kecil daripada gaya interaksi yang terjadi, dan oleh karenanya gaya tersebut diabaikan.

Jika energi kinetik total benda-benda setelah tumbukan sama dengan energi kinetik total benda-benda sebelum tumbukan, tumbukannya disebut tumbukan elastik sempurna . sebaliknya jika energi kinetik total kedua benda setelah tumbukan tidak sama dengan energi kinetik total kedua benda sebelum tumbukan , tumbukannya disebut tumbukan tak elastik atau tumbukan tak lenting.

1. Tumbukan lenting sempurna pada satu dimensi

Ingat ! jika pada tumbukan tidak terjadi kehilangan energi kinetik, maka tumbukan yang terjadi bersifat lenting sempurna. Disini akan dibahas tumbukan satu dimensi dimana kecepatan benda yang bertumbukan terletak segaris. Misalnya sepanjang sumbu-x seperti pada gambar 6 berikut:

Gambar 6. Ilustrasi 2 Bola Sebelum dan Sesudah Tumbukan

Berdasarkan Hukum Kekalan Momentum diperoleh;

atau

Oleh karena tumbukan yang terjadi adalah lenting sempurna, energi kinetiknya tetap, yaitu:

atau

Dengan mengingat,

Maka persamaan ketika terjadi tumbukan lenting sempurna dapat dituliskan sebagai berikut :

Jika persamaan tersebut dibagi dengan persamaan;

Maka diperoleh persamaan sebagai berikut:

2. Tumbukan lenting sempurna pada bidang

Tumbukan ini terjadi pada bidang dua dimensi yang tidak segaris, melainkan sebidang (dua dimensi). Contoh tumbukan semacam ini adalah tumbukan yang terjadi pada dua bola billiar atau tumbukan yang terjadi pada tumbukan dua mobil yang sejenis dan melaju dengan kecepatan yang sama seperti pada gambar 7. ;

Gambar 7. Ilustrasi 2 Bola

Bertumbukan Pada Bidang

Dengan menerapkan hukum kekekalan momentum pada arah sumbu x, diperoleh

Karena pada awalnya kedua benda tidak bergerak pada arah y, maka komponen momentum dari arah y bernilai nol;

Pada tumbukan lenting sempurna, harga koefisien restitusi adalah sebagai berikut:

3. Tumbukan tidak lenting

Dalam tumbukan ini, setelah tumbukan kedua benda akan bergerak bersama seperti pada gambar 8.

Gambar 8. Ilustrasi Tumbukan Tidak Lenting

Dengan demikian, Hukum kekekalan momentumnya berbentuk:

Dengan demikian, kecepatan kedua benda setelah tumbukan dapat dihitung dengan rumus:

Jika salah satu benda misalnya m2 semula diam, maka persamaanya menjadi:

Jadi, dengan hanya mengukur massa dan kecepatan sebelum tumbukan, kecepatan benda setelah tumbukan dapat diperhitungkan. Dalam tumbukan tidak lenting, energi kinetik setelah tumbukan selalu lebih kecil daripada energi kinetik sebelum tumbukan.

Rumus energi kinetik sebelum tumbukan adalah

Rumus energi kinetik setelah tumbukan adalah

Perbandingan enrgi kinetik setelah tumbukan dengan energi kinetik sebelum tumbukan adalah

Catatan: persamaan tersebut berlaku jika semula massa m2 diam.

Pada tumbukan tidak lenting, harga koefisien restitusi adalah sebagai berikut:

4. Tumbukan lenting sebagian

Sebagian besar tumbukan yang terjadi antara dua benda adalah tumbukan lenting sebagian. Misalnya, bola tenis yang bertumbukan dengan raket atau bola baseball yang dipukul. Analisis tumbukan tidak lenting sebagian melibatkan koefisien restitusi (e) .

koefisien restitusi didefinisikan sebagai harga negatif dari perbandingan antara besar kecepatan relatif kedua benda setelah tumbukan dan sebelum tumbukan.